Ejercicios resueltos de árbol de decisiones en Excel
Si estas buscando aprender más sobre toma de decisiones; quédate, aquí te presentamos 5 ejercicios resueltos de árbol de decisiones en Excel con sus respectivos archivos para descargar.
En estos ejercicios utilizamos el complemento de excel Simple Decision Tree; si aún no lo tienes, primero debes revisar esta entrada:
3 excelentes complementos de excel para hacer un árbol de decisiones
Encuentra mas ejercicios en: Ejercicios Resueltos de árboles de decisión
Ejercicio 1:
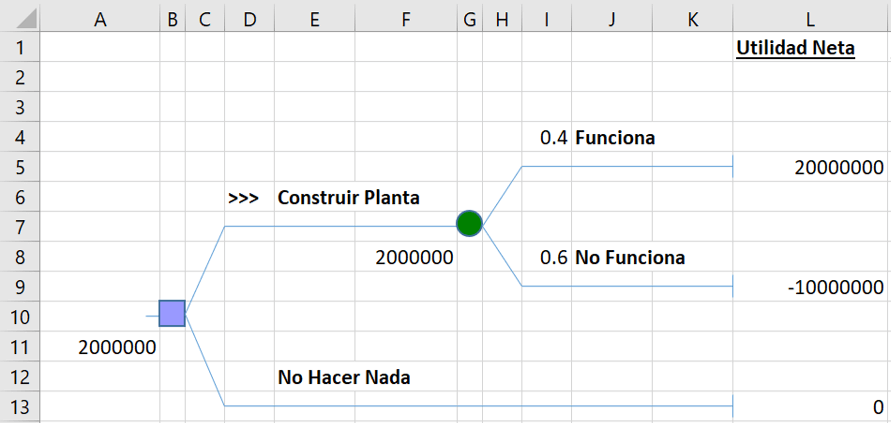
Benjamin Moses, jefe de ingenieros de Offshore Chemicals, Inc., tiene que decidir sobre la conveniencia de construir una nueva planta de procesamiento basada en una tecnología experimental. Si la nueva planta funciona bien, la compañía obtendrá una utilidad neta de $20 millones. Si la nueva planta fracasa, la compañía perderá $10 millones. Benjamin calcula que la probabilidad de que la nueva planta funcione satisfactoriamente es de 40%.
¿Qué decisión debe tomar Benjamin Moses?
Solución 1:
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
En este ejercicio no tenemos mayor inconveniente para hallar el valor de los nodos terminales; debido a que el enunciado los indica de forma directa.
De acuerdo al gráfico, inferimos que la mejor opción es construir la planta. Puedes descargar el archivo de la solución aquí: Ejercicio 1
Ejercicio 2:
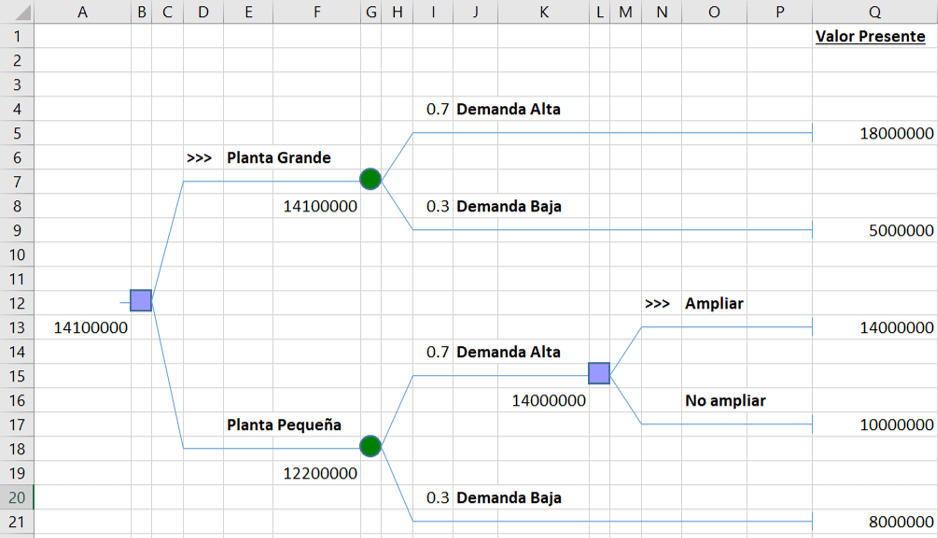
Una planta manufacturera ha alcanzado su plena capacidad. Ahora, la compañía tiene que construir una segunda planta, ya sea pequeña o grande, en un lugar cercano. La demanda futura podría ser alta o baja. La probabilidad de que sea baja es de 0.3. Si la demanda es baja, la planta grande tiene un valor presente de $5 millones y la planta pequeña, de $8 millones. Si la demanda es alta, a la planta grande corresponde un valor presente de $18 millones y a la planta pequeña, un valor presente de sólo $10 millones. Sin embargo, la planta pequeña puede ampliarse después en caso de que la demanda resulte ser alta, para alcanzar un valor presente de $14 millones.
- Dibuje un árbol de decisiones para este problema.
- ¿Qué debe hacer la gerencia para obtener el beneficio esperado más alto?
Solución 2:
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
En este ejercicio no tenemos mayor inconveniente para hallar el valor de los nodos terminales; debido a que el enunciado los indica de forma directa.
De acuerdo al gráfico, inferimos que la mejor opción es construir una planta grande desde el inicio. Puedes descargar el archivo de la solución aquí: Ejercicio 2
Ejercicio 3:
Una constructora encontró un terreno que quiere adquirir para construir en él más adelante. En la actualidad, el terreno está clasificado para contener cuatro casas por acre, pero piensa solicitar un cambio de clasificación. Lo que construya depende de la autorización del cambio que piensa solicitar y del análisis que usted haga de este problema para aconsejarla. Con la información del problema y la intervención de usted, el proceso de decisión se reduce a los costos, opciones y probabilidades siguientes:
Costo del terreno: 2 millones de dólares.
Probabilidad de cambio de clasificación: 0.60.
Las situaciones que se pueden presentar son:
-
- Si el terreno se reclasifica habrá 1 millón de dólares de costos adicionales por concepto de nuevas calles, alumbrado, etcétera.
- Si el terreno se reclasifica el contratista debe decidir si construye un centro comercial o 1 500 departamentos, como un plan tentativo muestra que sería factible.
- En caso decidan construir un centro comercial, existe 70% de probabilidad de que lo pueda vender a una cadena de tiendas de departamentos por 4 millones de dólares más que su costo de construcción, excluyendo el costo del terreno; y existe 30% de probabilidad de que lo pueda vender a una compañía aseguradora por 5 millones de dólares por encima de su costo de construcción (también excluyendo el terreno).
- En cambio, si en lugar del centro comercial decide construir los 1 500 departamentos, su cálculo de las probabilidades de utilidad son: 60% de probabilidad de vender los departamentos a una compañía de bienes raíces por 3 000 dólares cada uno por encima de su costo de construcción; 40% de probabilidad de que solo obtenga 2 000 dólares de cada uno sobre su costo de construcción (los dos excluyen el costo del terreno).
- Si el terreno no se reclasifica, se cumplirá con las restricciones existentes de la clasificación actual y simplemente construirá 600 casas, en cuyo caso espera ganar 4 000 dólares sobre el costo de construcción por cada una (excluyendo el costo del terreno).
Prepare un árbol de decisión del problema y determine la mejor solución y la utilidad neta esperada.
Solución 3:
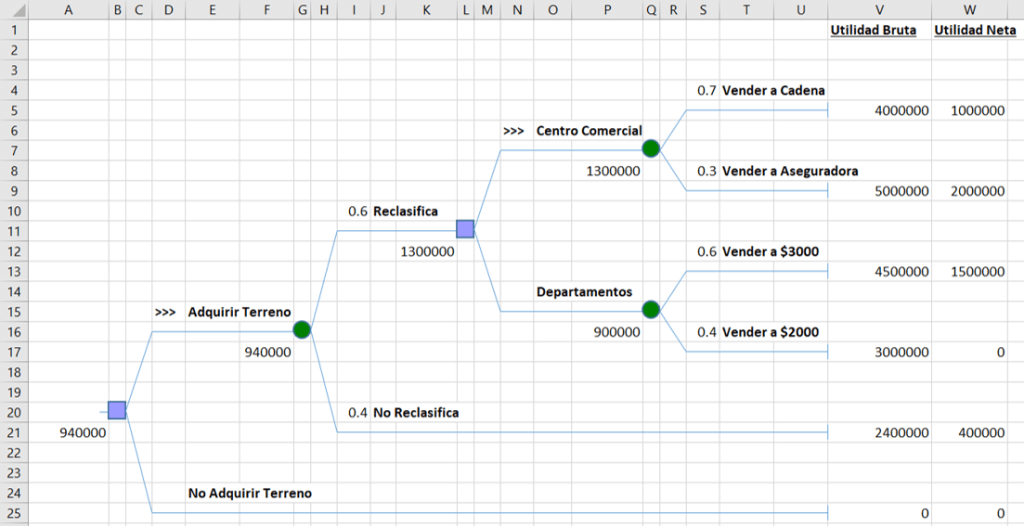
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
En la parte final del árbol puedes ver dos columnas que representan la utilidad:
- La utilidad bruta representa la utilidad de la empresa en cada nodo, sin contar los costos del terreno.
- La utilidad neta, es la utilidad de la empresa descontando los costos del terreno. Los cálculos de los nodos intermedios se obtienen con los valores de esta columna.
De acuerdo al gráfico, inferimos que la mejor opción es adquirir el terreno; y en caso se reclasifique, se debe construir un centro comercial. Puedes descargar el archivo de la solución aquí: Ejercicio 3
Ejercicio 4:
McBurger, Inc., desea rediseñar sus cocinas para mejorar la productividad y la calidad. Tres diseños, denominados K1, K2 y K3, están bajo consideración. Sin importar cuál diseño se use, la demanda diaria de emparedados en un restaurante típico McBurger es de 500. Producir un emparedado cuesta $1.30. Los emparedados no defectuosos se venden en promedio a $2.50 cada uno; los defectuosos no se pueden vender y son desechados.
La meta es elegir un diseño que maximice la ganancia esperada en un restaurante típico durante un periodo de 300 días. Los diseños K1, K2 y K3 cuestan $100,000, $130,000 y $180,000, respectivamente y se esperan los siguientes resultados:
- Bajo el diseño K1, hay una probabilidad de 0.80 de que 90 de cada 100 emparedados sean no defectuosos, y una probabilidad de 0.20 de que 70 de cada 100 sean no defectuosos.
- Con el diseño K2, hay una probabilidad de 0.85 de que 90 de cada 100 emparedados sean no defectuosos, y una probabilidad de 0.15 de que 75 de cada 100 sean no defectuosos.
- Bajo el diseño K3, hay una probabilidad de 0.90 de que 95 de cada 100 emparedados sean no defectuosos, y una probabilidad de 0.10 de que 80 de cada 100 sean no defectuosos.
¿Cuál es el nivel de ganancia esperado para el diseño que alcanza el máximo nivel de ganancias esperadas durante 300 días?
Solución 4:
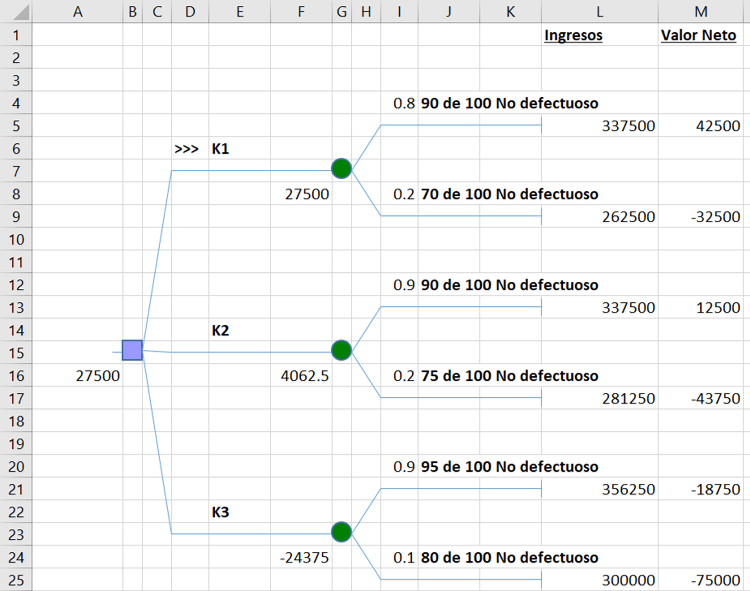
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
En la parte final del árbol puedes ver dos columnas con las siguiente denominaciones:
- Los ingresos de cada nodo, que se calculan de la siguiente manera:
(Demanda Diaria) x (N° de Días) x (Precio de Venta) x (Fracción de No defectuosos)
(500) x (300) x (2.50) x (Fracción de No defectuosos)
- El valor neto, es la utilidad neta de cada nodo restando los ingresos menos los costos. Los costos se calculan de la siguiente manera:
Costo de Diseño + [(Demanda Diaria) x (N° de Días) x (Costo de Producción)]
Costo de Diseño + (500) x (300) x (1.30)
Los cálculos de los nodos intermedios se obtienen con los valores de la última columna (Valor Neto).
De acuerdo al gráfico, inferimos que la mejor opción es elegir el diseño K1. Puedes descargar el archivo de la solución aquí: Ejercicio 4
Ejercicio 5:
Los negocios de Acme Steel Fabricators han sido muy prósperos en los últimos cinco años. La compañía fabrica una amplia gama de productos de acero, como barandales, escaleras y marcos de acero estructural ligero. El método manual vigente para manejo de materiales ocasiona un exceso de inventario y congestionamientos. Acme está considerando si debe comprar un sistema de transporte que pende de un riel, o un vehículo montacargas, para incrementar su capacidad y mejorar su eficiencia manufacturera.
Los resultados anuales del sistema, antes de impuestos, dependen de la demanda futura. Si la demanda se mantiene en el nivel actual, lo cual tiene una probabilidad de 0.50, el ahorro anual que producirá el transportador elevado será de $10,000. Si la demanda aumenta, el transportador permitirá ahorrar $25,000 al año por la eficiencia operativa, además de las nuevas ventas. Finalmente, si la demanda cae, el transportador provocará una pérdida anual estimada en $65,000.
Se estima una probabilidad de 0.30 de que la demanda sea alta y de 0.20 de que sea baja.
Si se compra, el montacargas, los resultados anuales serán de $5,000 si la demanda no cambia, $10,000 si la demanda aumenta y –$25,000 si la demanda cae.
- Dibuje un árbol de decisiones para este problema y calcule el valor esperado de los resultados de cada alternativa.
- ¿Cuál es la mejor alternativa, con base en los valores esperados?
Solución 5:
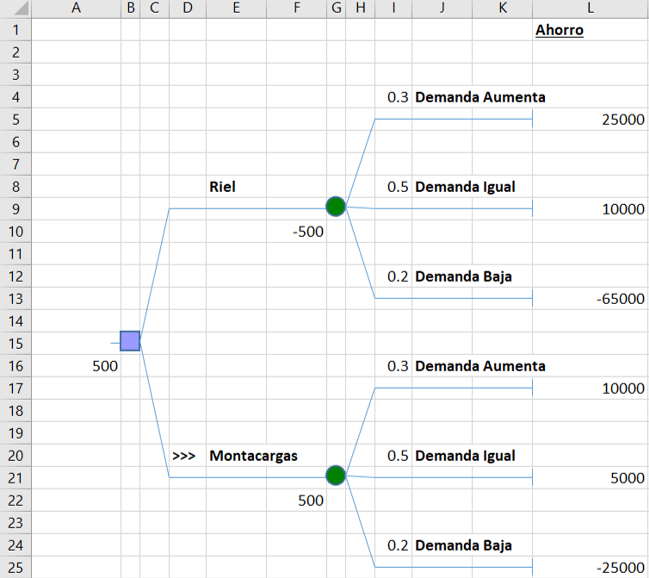
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
En este ejercicio no tenemos mayor inconveniente para hallar el valor de los nodos terminales; debido a que el enunciado los indica de forma directa.
De acuerdo al gráfico, inferimos que la mejor opción es adquirir un montacargas. Puedes descargar el archivo de la solución aquí: Ejercicio 5
Reflexión Final
Como puedes ver, el usar Simple Decision Tree en Excel facilita enormemente la elaboración de nuestros árboles de decisiones.
Si tienes alguna duda al respecto te invitamos a dejarla en los comentarios. Finalmente, si deseas revisar ejercicios resueltos sobre otros temas, puedes ubicarlos aquí: Ejercicios Resueltos.
Referencias:
Los ejercicios presentados han sido tomados de los siguientes libros:
- Chase, R. & Jacobs, F. (2014). Administración de operaciones. Producción y cadena de suministro (Decimotercera ed.). Mexico, D.F.: McGraw-Hill.
- Heizer, J., & Render, B. (2014). Principios de Administración de Operaciones (Novena ed.). Mexico, D.F.: Pearson Educación.
- Krajewski, L., Ritzman, L. & Malhotra M, (2008). Administración de Operaciones. Procesos y Cadena de Valor (Octava ed.). Mexico, D.F.: Pearson Educación.