Ejercicios resueltos de árbol de decisiones
Los árboles de decisión son una herramienta poderosísima para la toma de decisiones en las empresas; es por ello que en esta entrada te presentamos 5 ejercicios resueltos de árbol de decisiones para que aprendas a elaborarla.
Si aún tienes algunas dudas sobre la elaboración de los árboles de decisiones, debes revisar nuestra entrada: Cómo elaborar un árbol de decisiones paso a paso+ejemplos.
Te recomendamos ver también: El mejor programa online gratis para hacer un diagrama de árbol de decisiones
Encuentra mas ejercicios en: Ejercicios Resueltos de árbol de decisiónes en excel
Ejercicio 1:
El grupo de diseño del producto de Flores Electric Supplies, Inc., ha determinado que necesita diseñar una nueva serie de interruptores. Debe decidirse por una de las tres estrategias de diseño. El pronóstico del mercado es para 200,000 unidades. Cuanto mejor y más sofisticada sea la estrategia de diseño y mayor el tiempo invertido en ingeniería de valor, menor será el costo variable.
El jefe de ingeniería de diseño, Dr. W. L. Berry, decidió que los siguientes costos son una buena estimación de los costos iniciales y variables relacionados con cada una de las tres estrategias:
- Baja tecnología: proceso con poca tecnología y bajo costo que consiste en contratar a nuevos ingenieros con poca experiencia. Esta posibilidad tiene un costo de $45,000 y probabilidades de costo variable de 0.3 para $0.55 cada uno, 0.4 para $0.50, y .3 para $0.45.
- Subcontrato: enfoque de mediano costo que emplea un buen equipo de diseño externo. Esta alternativa tendría un costo inicial de $65,000 y probabilidades de costo variable de 0.7 para $0.45 cada uno, 0.2 para $0.40, y 0.1 para $0.35.
- Alta tecnología: enfoque de alta tecnología en el que se usa lo mejor del personal interno y la más moderna tecnología de diseño asistido por computadora. Esta alternativa tiene un costo inicial de $75,000 y probabilidades de costo variable de 0.9 para $.40 y 0.1 para $0.35.
¿Cuál es la mejor decisión con base en un criterio de valor monetario esperado (VME)? (Nota: Queremos el VME más bajo puesto que se manejan costos en este problema).
Solución 1:
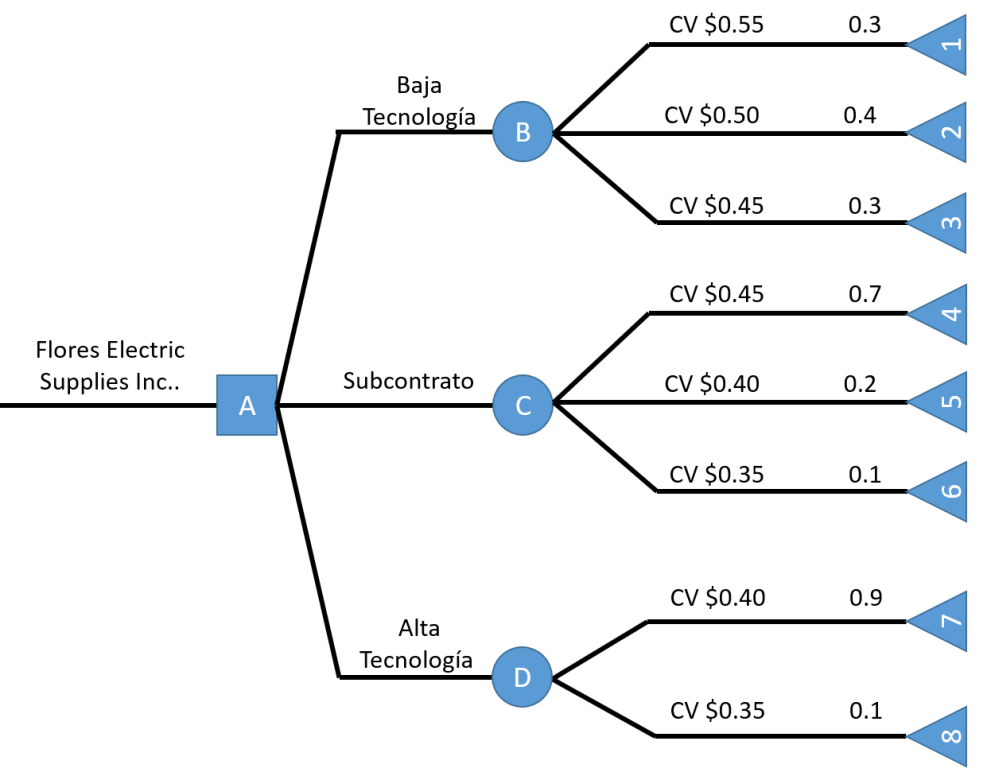
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
CV = Costo Variable
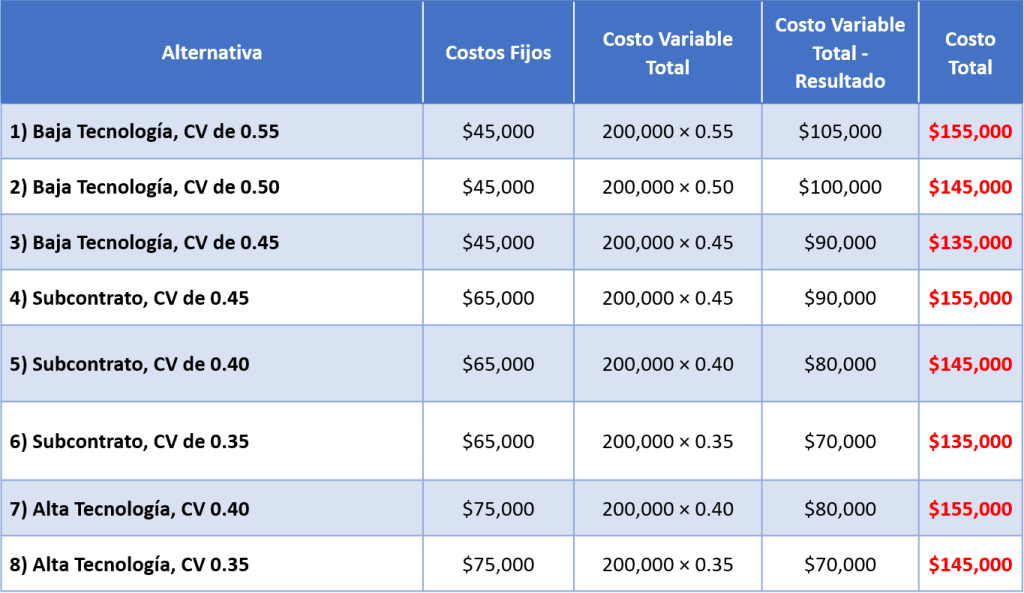
Procedemos a calcular los extremos de los nodos de nuestro árbol:
El costo total se obtiene sumando el costo fijo mas el costo variable total; teniendo en cuenta el pronóstico del mercado de 200,000 unidades.
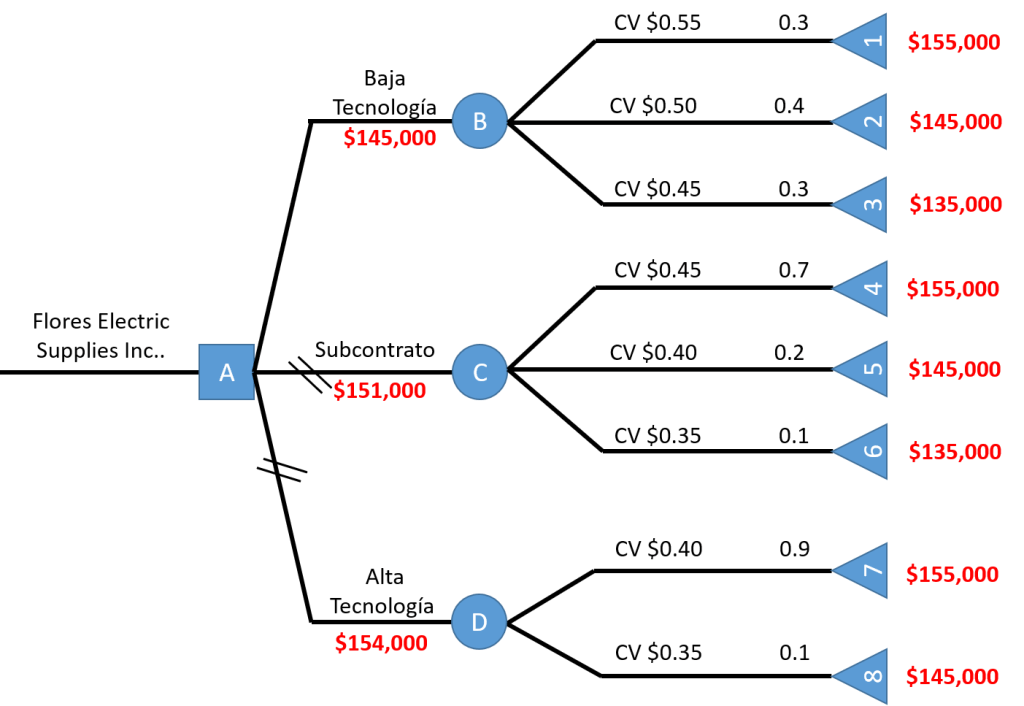
Finalmente calculamos los valores de los nodos intermedios y marcamos con 2 líneas las alternativas rechazadas.
Como evaluamos el costo total de las estrategias que evalúa la empresa; elegiremos la alternativa con valor monetario esperado: Baja Tecnología.
Ejercicio 2:
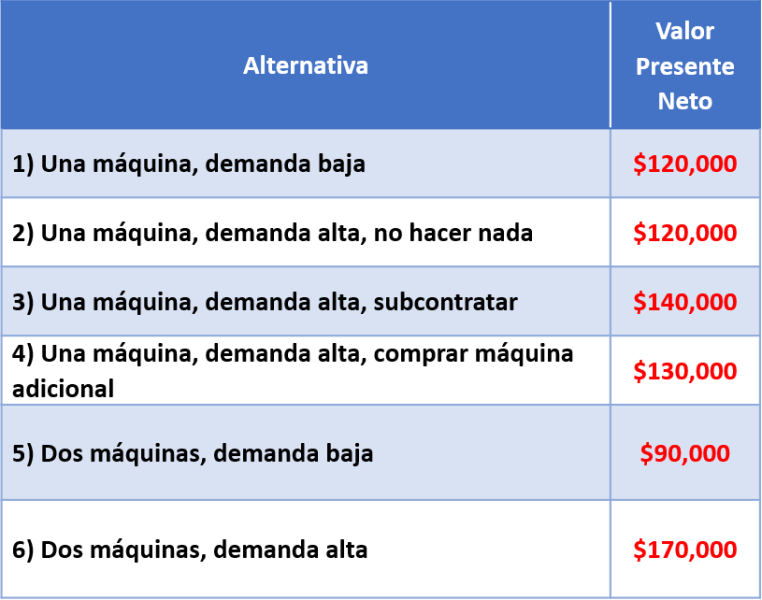
Un gerente está tratando de decidir si debe comprar una máquina o dos. Si compra sólo una y la demanda resulta ser excesiva, podría adquirir después la segunda máquina. Sin embargo, perdería algunas ventas porque el tiempo que implica la fabricación de este tipo de máquinas es de seis meses. Además, el costo por máquina sería más bajo si comprara las dos al mismo tiempo. La probabilidad de que la demanda sea baja se ha estimado en 0.30. El valor presente neto, después de impuestos, de los beneficios derivados de comprar las dos máquinas a la vez es de $90,000 si la demanda es baja, y de $170,000 si la demanda es alta.
Si se decide comprar una máquina y la demanda resulta ser baja, el valor presente neto sería de $120,000. Si la demanda es alta, el gerente tendrá tres opciones. La de no hacer nada tiene un valor presente neto de $120,000; la opción de subcontratar, $140,000; y la de comprar la segunda máquina, $130,000.
- Dibuje un árbol de decisiones para este problema.
- ¿Cuántas máquinas debe comprar la compañía inicialmente? ¿Cuál es el beneficio esperado de esta alternativa?
Solución 2:
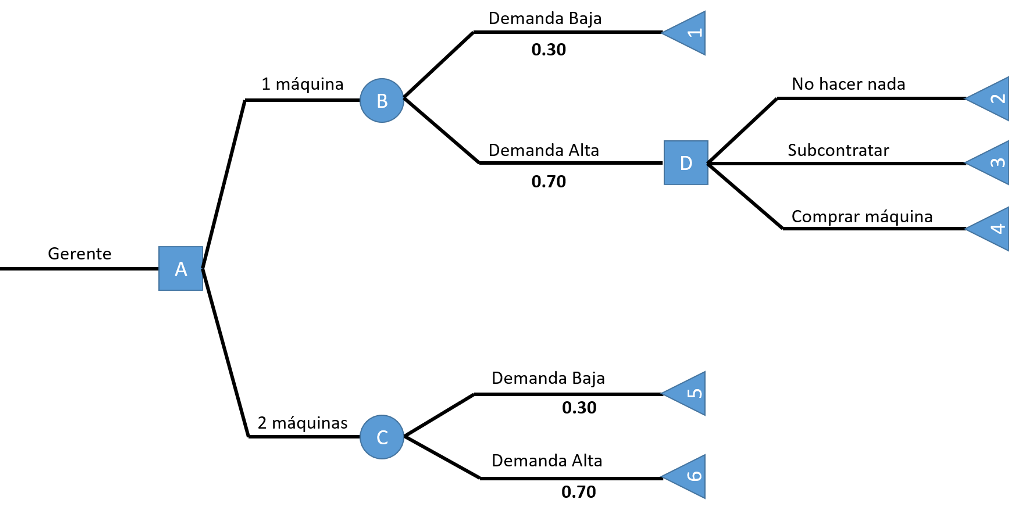
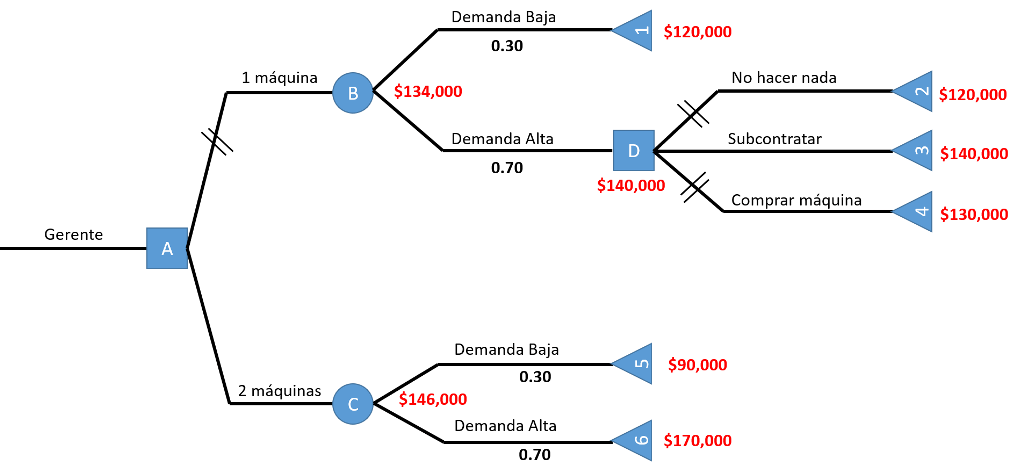
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
Procedemos a calcular los extremos de los nodos de nuestro árbol:
Finalmente calculamos los valores de los nodos intermedios y marcamos con 2 líneas las alternativas rechazadas; quedando nuestro árbol de la siguiente manera:
La compañía debe comprar dos máquinas que representa un beneficio esperado de $146,000.
Ejercicio 3:
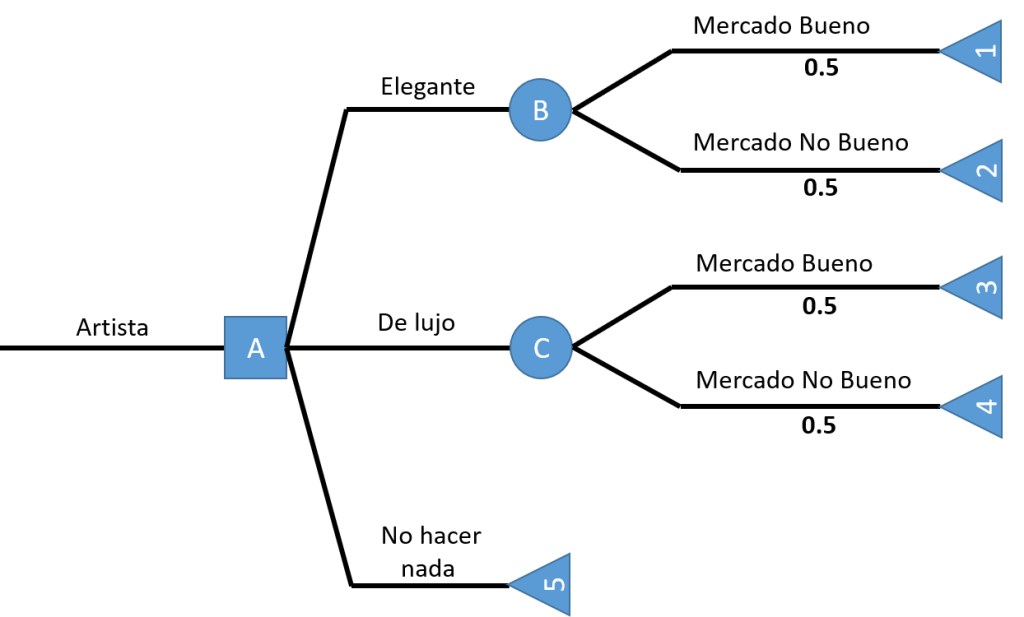
Los residentes de Mili River tienen hermosos recuerdos del patinaje sobre hielo en el parque local. Un artista captó la experiencia en un dibujo y espera reproducirlo y vender las copias enmarcadas a los residentes actuales y anteriores. El artista considera que si el mercado es bueno podría vender 400 copias de la versión elegante a $125 cada una. Si el mercado no es bueno, sólo vendería 300 copias a $90 cada una. O puede hacer una versión de lujo del mismo dibujo. Cree que si el mercado fuera bueno podría vender 500 copias de la versión de lujo a $100 cada una. Si el mercado no es bueno podría vender 400 copias a $70 cada una. En ambos casos, los costos de producción serán aproximadamente de $35,000.
También puede no hacer los cuadros esta vez. Pero si considera que hay un 50% de probabilidades de tener un buen mercado, ¿qué debe hacer? ¿Por qué?
Solucion 3:
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
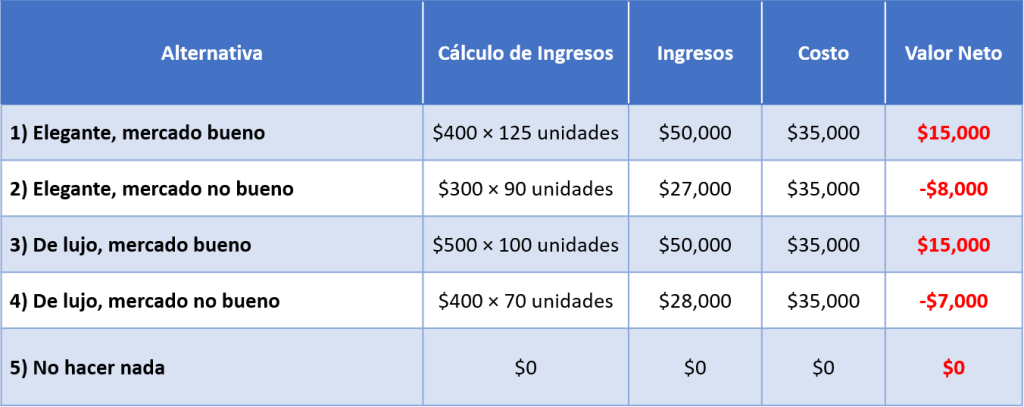
Procedemos a calcular los extremos de los nodos de nuestro árbol:
En este ejercicio tenemos algunos nodos que tienen valor negativo; sin embargo, el procedimiento se realiza de la misma forma; incluyendo el signo correspondiente en los cálculos. Por ejemplo el valor del nodo B sería:
15,000 × 0.5 + (-8,000)×0.5 = 3,500
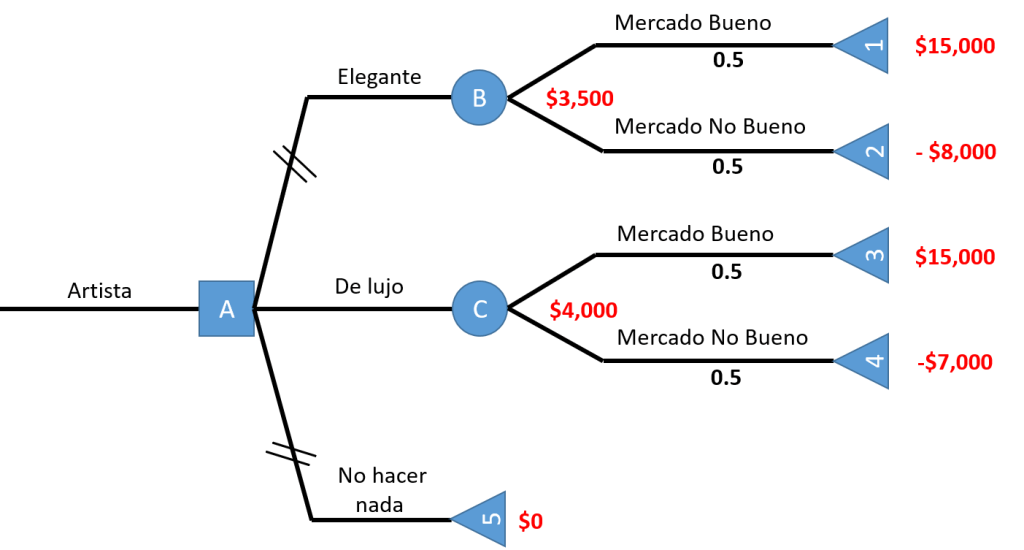
Finalmente calculamos los valores de los otros nodos y marcamos con 2 líneas las alternativas rechazadas; quedando nuestro árbol de la siguiente manera:
El artista debe decantarse por hacer la versión de lujo que tiene mayor valor monetario esperado.
Ejercicio 4:
Un gerente trata de decidir si debe construir una instalación pequeña, mediana o grande. La demanda puede ser baja, promedio o alta, con probabilidades estimadas de 0.25, 0.40 y 0.35, respectivamente.
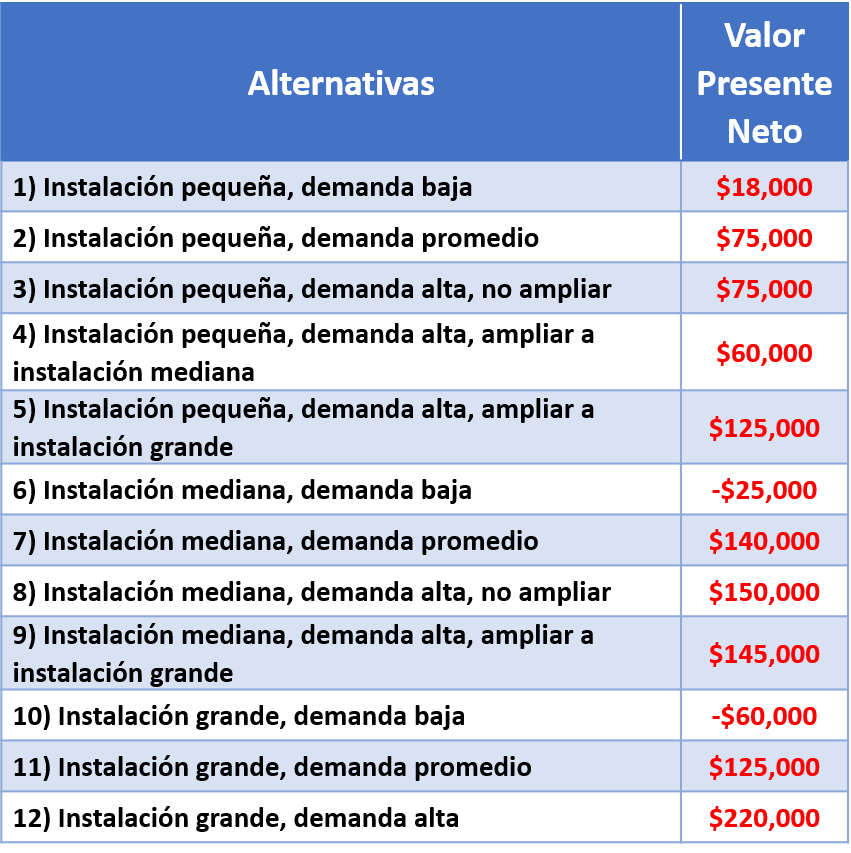
Con una instalación pequeña se esperaría ganar un valor presente neto, después de impuestos, de sólo $18,000 si la demanda es baja. Si la demanda es promedio, se espera que la instalación pequeña gane $75,000. Si la demanda es alta, cabría esperar que la instalación pequeña ganara $75,000 y que después pudiera ampliarse a un tamaño promedio para ganar $60,000, o a un tamaño grande para ganar $125,000.
Con una instalación de tamaño mediano se esperaría una pérdida estimada en $25,000 si la demanda es baja, y una ganancia de $140,000 si la demanda es de magnitud promedio. Si la demanda es alta, cabría esperar que la instalación de tamaño mediano ganara un valor presente neto de $150,000; después podría ampliarse al tamaño grande para obtener un beneficio neto de $145,000.
Si se optara por construir una instalación grande y la demanda resultara ser alta, se esperaría que las ganancias ascendieran a $220,000. Si la demanda resultara ser de magnitud promedio para la instalación grande, se esperaría que el valor presente neto fuera igual a $125,000; finalmente si la demanda fuera baja, cabría esperar que la instalación perdiera $60,000.
- Dibuje un árbol de decisiones para este problema.
- ¿Qué debe hacer la gerencia para obtener el beneficio esperado más alto?
Solución 4:
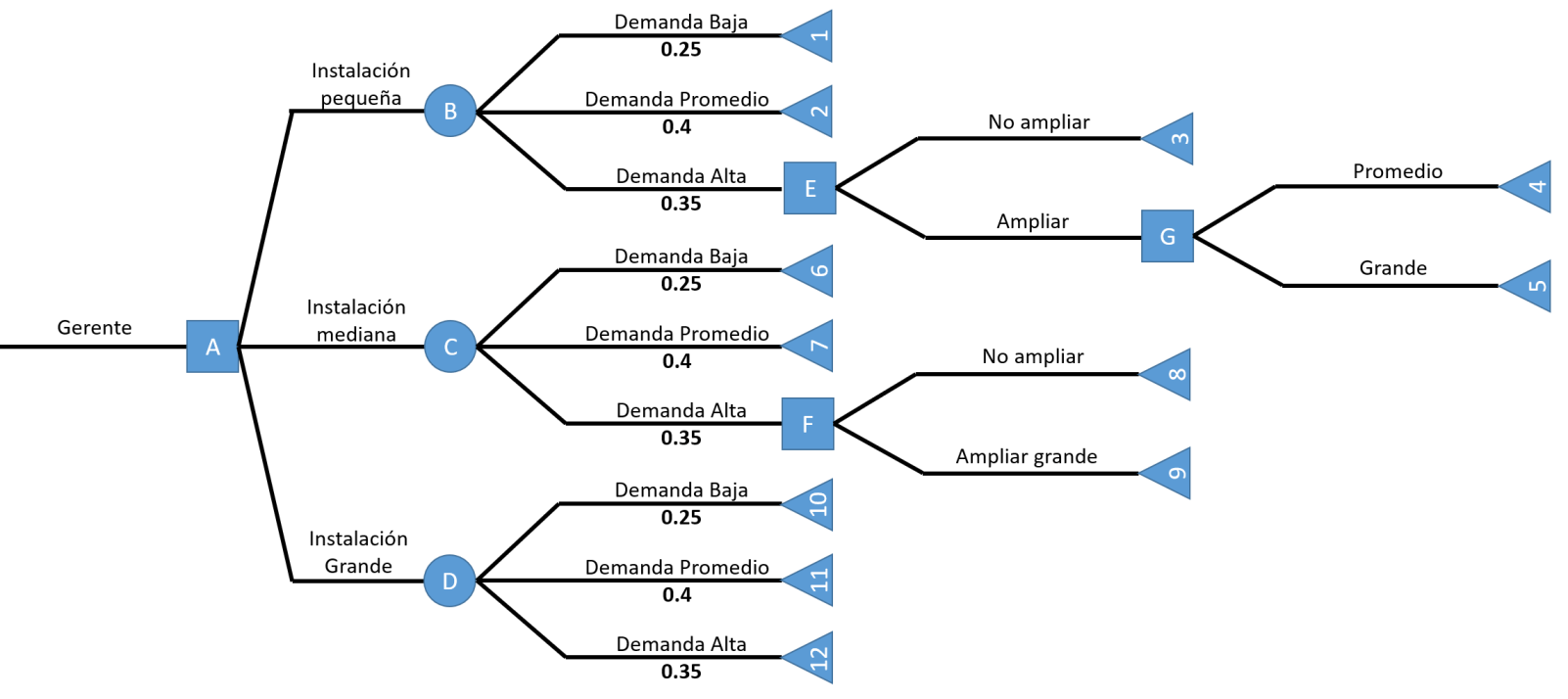
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
Procedemos a calcular los extremos de los nodos de nuestro árbol:
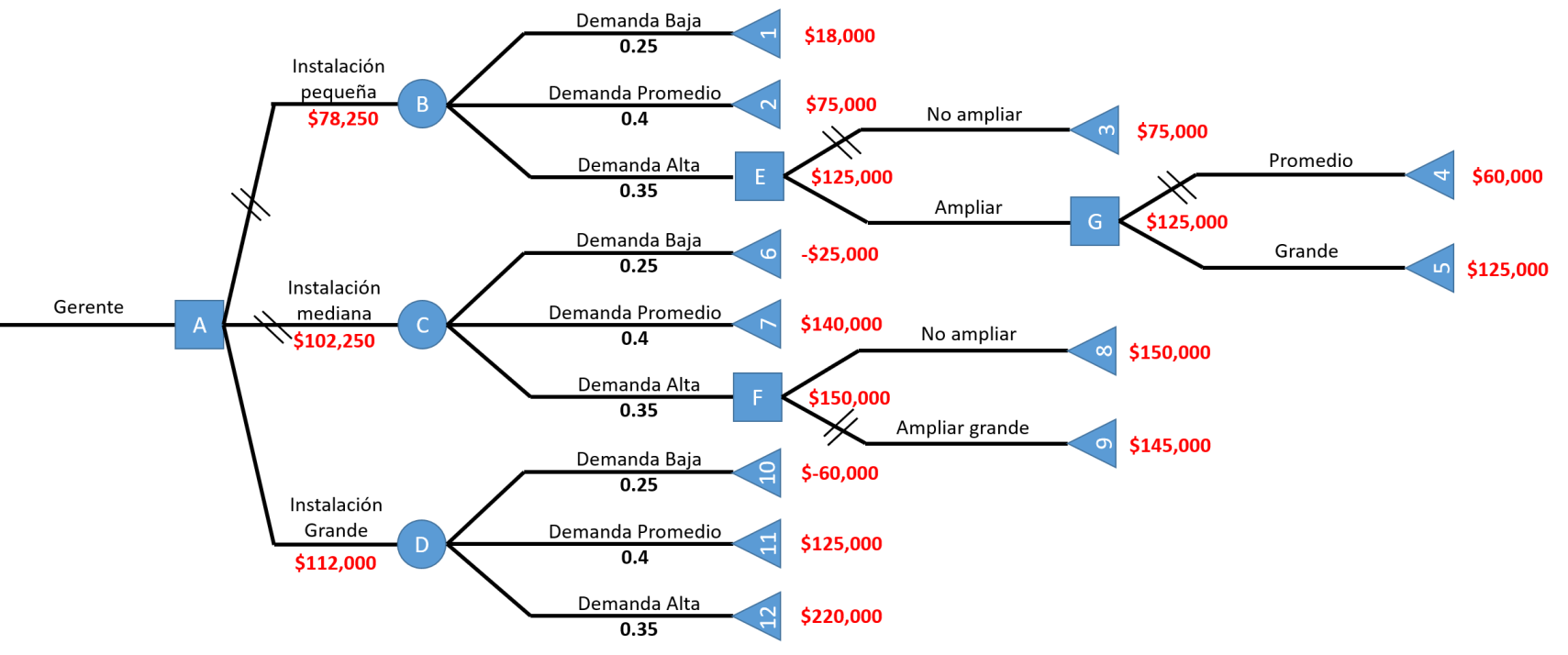
Finalmente calculamos los valores de los otros nodos y marcamos con 2 líneas las alternativas rechazadas; quedando nuestro árbol de la siguiente manera:
La gerencia debe construir una instalación grande desde el inicio ya que representa el mayor valor monetario esperado.
Ejercicio 5:
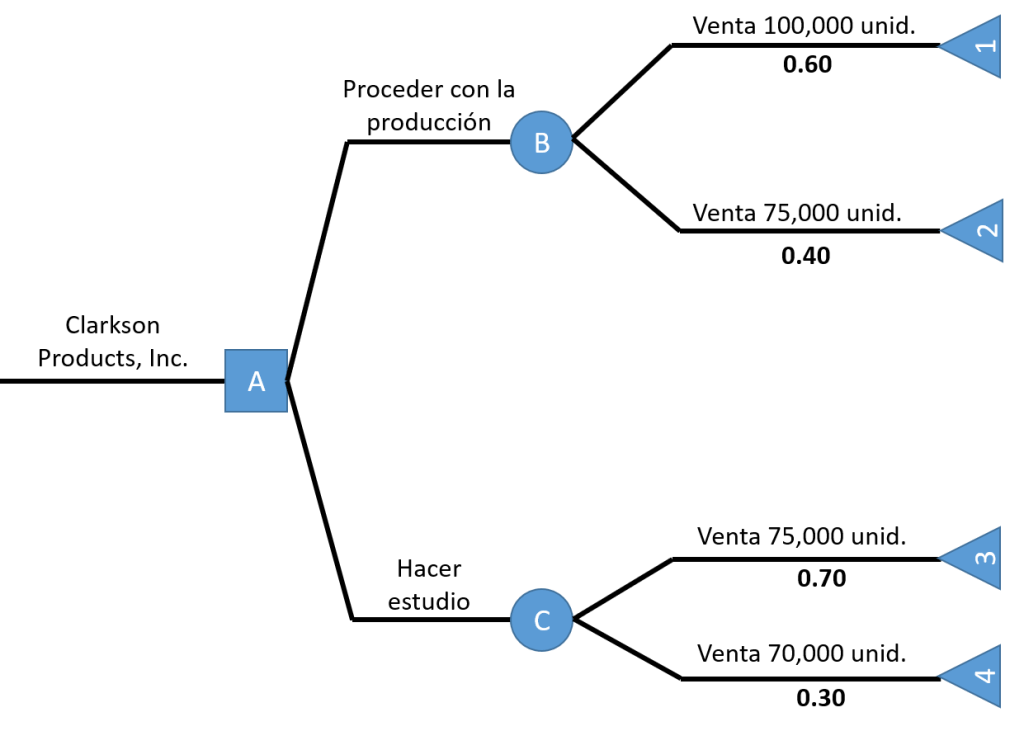
Clarkson Products, Inc., de Clarkson, Nueva York, tiene la posibilidad de (a) proceder de inmediato con la producción de una nueva televisión estereofónica de la más alta calidad, de la cual acaba de completar la prueba del prototipo o, (b) hacer que el equipo de análisis de valor complete el estudio. Si Ed Lusk, vicepresidente de operaciones, procede con el prototipo existente (opción a), la empresa puede esperar que las ventas lleguen a 100,000 unidades a $550 cada una, con una probabilidad de 0.6 y una de 0.4 para 75,000 a $550. No obstante, si utiliza al equipo de análisis de valor (opción b), la empresa espera ventas por 75,000 unidades a $750 cada una, con una probabilidad de 0.7 y una de 0.3 para 70,000 unidades a $750. El costo del análisis de valor es de $100,000 si sólo se usa en la opción b.
¿Cuál de las dos alternativas tiene el valor monetario esperado (VME) más alto?
Solución 5:
Elaboramos el árbol de decisión según las opciones que nos muestra el problema:
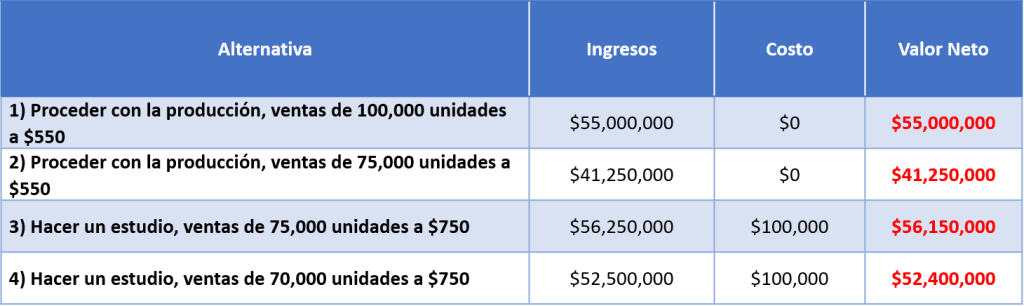
Procedemos a calcular los extremos de los nodos de nuestro árbol:
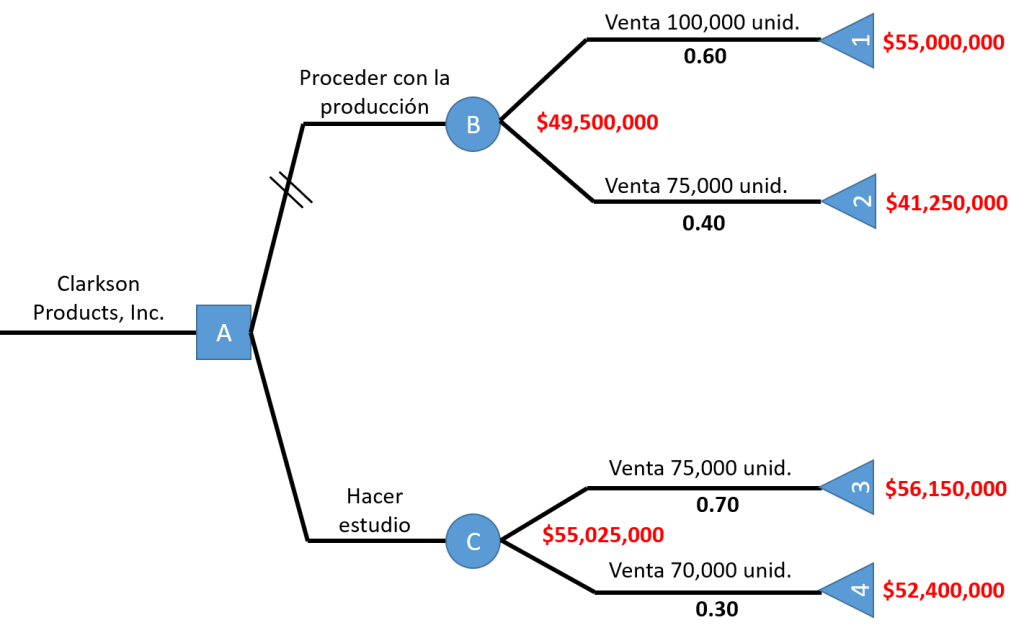
Finalmente calculamos los valores de los otros nodos y marcamos con 2 líneas las alternativas rechazadas; quedando nuestro árbol de la siguiente manera:
La empresa debe realizar el prueba del prototipo antes de salir al mercado, de esa forma podrá tener un mayor valor monetario esperado.
Reflexión Final
Estoy seguro que con los ejercicios resueltos que hemos presentado, podrás evaluar diferentes alternativas con los árboles de decisión para tomar mejores decisiones.
Si tienes alguna duda al respecto te invitamos a dejarla en los comentarios. Finalmente, si deseas revisar ejercicios resueltos sobre otros temas, puedes ubicarlos aquí: Ejercicios Resueltos.
Referencias:
Los ejercicios presentados han sido tomados de los siguientes libros:
- Chase, R. & Jacobs, F. (2014). Administración de operaciones. Producción y cadena de suministro (Decimotercera ed.). Mexico, D.F.: McGraw-Hill.
- Heizer, J., & Render, B. (2014). Principios de Administración de Operaciones (Novena ed.). Mexico, D.F.: Pearson Educación.
- Krajewski, L., Ritzman, L. & Malhotra M, (2008). Administración de Operaciones. Procesos y Cadena de Valor (Octava ed.). Mexico, D.F.: Pearson Educación.