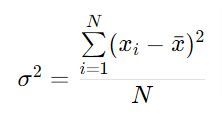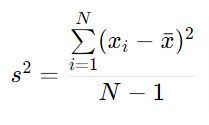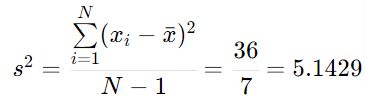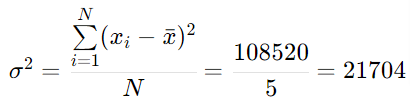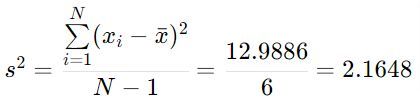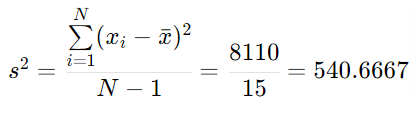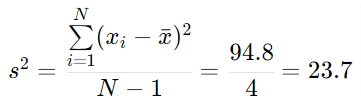Ejemplos de la varianza estadística – Ejercicios Resueltos paso a paso

La varianza es uno de los conceptos más importantes en la estadística y es de aprendizaje obligatorio para todos los profesionales relacionados con la gestión empresarial. Es por ello que en este artículo te presentamos ejemplos resueltos de la varianza estadística con explicaciones paso a paso.

En los ejemplos que solucionaremos se han incluido ejercicios sobre la varianza poblacional y muestral. Los resultados de los problemas se han obtenido utilizando nuestra calculadora online de la varianza.

Antes de iniciar, te recordamos las fórmulas para calcular la varianza:

a) Varianza Poblacional:

b) Varianza Muestral:

Donde:

• σ²: Varianza Poblacional.
• s²: Varianza Muestral.
• x̄: Media.
• N: Cantidad de valores evaluados.
• x_i: Cada uno de los valores.

Ejercicio 1:

Calcule la varianza de los siguientes datos muestrales: 6, 8, 7, 10, 3, 5, 9, 8

Solución 1:

De acuerdo a los datos del problema tenemos:

• Σxᵢ = 56
• N = 8
• x̄ = 56/8 = 7

xi	xi – x̄	(xi – x̄)2
6	-1	1
8	1	1
7	0	0
10	3	9
3	-4	16
5	-2	4
9	2	4
8	1	1
Σxᵢ = 56	x̄ = 56/8 = 7	Σ(xᵢ – x̄)² = 36

Finalmente calculamos la varianza muestral:

Ejercicio 2:

Un grupo de amigos miden la altura de sus perros (en milímetros):

Las alturas (hasta los hombros) son: 600 mm, 470 mm, 170 mm, 430 mm y 300 mm. Calcule la varianza.

Solución 2:

De acuerdo a los datos del problema tenemos:

• Σxᵢ = 1970
• N = 5
• x̄ = 1970/5 = 394

xi	xi – x̄	(xi – x̄)2
600	206	42436
470	76	5776
170	-224	50176
430	36	1296
300	-94	8836
Σxᵢ = 1970	x̄ = 1970/5 = 394	Σ(xᵢ – x̄)² = 108520

Finalmente calculamos la varianza poblacional:

Ejercicio 3:

Los rendimientos porcentuales anuales de las letras del Tesoro de Estados Unidos fueron los siguientes: 6.5%, 4.4%, 3.8%, 6.9%, 8.0%, 5.8%, 5.1%. Calcule la varianza muestral:

Solución 3:

De acuerdo a los datos del problema tenemos:

• Σxᵢ = 40.5
• N = 7
• x̄ = 40.5/7 = 5.7857

xi	xi – x̄	(xi – x̄)2
6.5	0.7143	0.5102
4.4	-1.3857	1.9202
3.8	-1.9857	3.943
6.9	1.1143	1.2417
8	2.2143	4.9031
5.8	0.0143	0.0002
5.1	-0.6857	0.4702
Σxᵢ = 40.5	x̄ = 40.5/7 = 5.7857	Σ(xᵢ – x̄)² = 12.9886

Finalmente calculamos la varianza muestral:

Ejercicio 4:

Encuentre la varianza para la siguiente muestra: 12, 13, 24, 24, 25, 26, 34, 35, 38, 45, 46, 52, 53, 78, 78, 89

Solución 4:

De acuerdo a los datos del problema tenemos:

• Σxᵢ = 672
• N = 16
• x̄ = 672/16 = 42

xi	xi – x̄	(xi – x̄)2
12	-30	900
13	-29	841
24	-18	324
24	-18	324
25	-17	289
26	-16	256
34	-8	64
35	-7	49
38	-4	16
45	3	9
46	4	16
52	10	100
53	11	121
78	36	1296
78	36	1296
89	47	2209
Σxᵢ = 672	x̄ = 672/16 = 42	Σ(xᵢ – x̄)² = 8110

Finalmente calculamos la varianza muestral:

Puedes ver la solución con la calculadora en este enlace.

Ejercicio 5:

Halla la varianza de las temperaturas medias registradas durante un periodo de cinco días del pasado invierno: 18, 22, 19, 25, 12.

Solución 5:

De acuerdo a los datos del problema tenemos:

• Σxᵢ = 96
• N = 5
• x̄ = 96/5 = 19.2

xi	xi – x̄	(xi – x̄)2
18	-1.2	1.44
22	2.8	7.84
19	-0.2	0.04
25	5.8	33.64
12	-7.2	51.84
Σxᵢ = 96	x̄ = 96/5 = 19.2	Σ(xᵢ – x̄)² = 94.8

Finalmente calculamos la varianza muestral:

Reflexión Final

Como hemos visto a lo largo de los ejemplos, obtener la varianza no es complicado, por el contrario, puedes aprender a calcularlo siguiendo cada uno de los pasos mostrados. Para poder llevar estos ejemplos siempre contigo puedes guardarlo en tu archivo como pdf con la opción de Imprimir (Ctrl+P).

Te recordamos que si quieres practicar en el cálculo de la desviación estándar, puedes visitar nuestro artículo de ejemplos de la desviación típica.

Si tienes alguna duda, sugerencia o consulta, te invitamos a mencionarlo en los comentarios; también puedes formar parte de nuestro grupo de Facebook, donde estaremos brindando contenido de calidad para todos los integrantes.

Dale like a nuestra Fan Page y suscríbete en nuestro canal de Youtube para enterarte de nuestras últimas novedades. Somos Plan de Mejora, el mejor lugar para aprender, crecer y mejorar.